Natuur en Techniek bij de Onderwijsvernieuwingscoöperatie (5)

De Onderwijsvernieuwingscoöperatie.nl (OVC) wil scholen voor aanvang van het schooljaar 2009-2010 voor de eerste twee leerjaren van het VO gedigitaliseerd leerboekvervangend leermateriaal aanreiken. Voor leerjaar 1 hebben de leermateriaalarrangeurs (LMA’s) al heel wat in de matrix staan voor de uitprobeerfase. Docenten kunnen het leermateriaal van hun vakcollega’s beoordelen en eventueel voorzetten aan hun leerlingen (http://www.inhetonderwijs.com/showcontent/). In het domein Natuur en Techniek bevindt zich wiskunde voor de onderbouw.

In de Informatiebrochure 'Digitaal leermateriaal arrangeren in de OVC' is hoofdstuk 6 gewijd aan Natuur en Techniek en Wiskunde in de onderbouw. Er is uitgegaan van de kerndoelen en de huidige leerstof van de basisvorming. De onderwerpen daarvan werden verbonden met concrete thema’s, die in de matrix werden gezet. Alle leerstof zoals die in de basisvorming wordt behandeld is in de thema’s opgenomen.
’De projectgroep maakt leerboekvervangend leermateriaal dat enerzijds alle kerndoelen dekt en anderzijds flexibel is in te zetten in iedere onderwijsvorm. Met een eenheid kan 50 minuten leertijd of meer worden gerealiseerd. Of die leertijd ingevuld wordt door middel van klassikaal onderwijs of in meer of mindere mate door middel van zelfstudie, is afhankelijk van het pedagogisch-didactisch systeem waar een school voor kiest. De geproduceerde eenheden zijn op dit moment zonder aanpassing op HAVO en VMBO-T niveau te gebruiken. Te zijner tijd zal in overleg met gebruikers, gewerkt gaan worden aan aanpassingen van het materiaal waardoor het breed inzetbaar wordt in alle schoolsoorten. Het materiaal heeft een vaste leerpsychologische opbouw: oriëntatie, leerdoelen, aanpak, beginsituatie, leeractiviteiten, beoordeling, reflectie’.

wiskunde

Zoals bij alle vakken geeft de matrix veel informatie over het domein, de kerndoelen, de status van het leermateriaal, het thema, de leereenheden, het leerjaar en niveau van de leerstof, de benodigde contacturen en de leermiddelenarrangeur die verantwoordelijk is voor de leereenheid.   
Voor het eerste leerjaar laat auteur Hendrik-Jan Timmerije de leerlingen digitaal oefenen met o.a. ruimtefiguren. De leerlingen beginnen met zich te oriënteren op het onderwerp. Ze krijgen een tekstje uit Wikepedia voorgezet waarin ze enkele ruimtefiguren en de toepassingen daarvan moeten opzoeken. Als voorbeeld krijgen ze mee de kubus met zijn toepassing de dobbelsteen.
Na de oriëntatie volgen de leerdoelen. Daar zien de leerlingen wat ze na de lessen over een zestal ruimtefiguren hebben geleerd en wat ze ermee moeten kunnen. Na de opdracht om de kenmerken van getekende ruimtefiguren te bestuderen, volgt een korte cloze test waarin de leerlingen moeten aangeven hoeveel hoekpunten een balk heeft, hoeveel vlakken en ribben een kubus enzovoort. Ze kunnen de duidelijk geformuleerde digitale opdrachten geheel zelfstandig uitvoeren. De oefeningen zijn interactief zodat ze meteen kunnen zien of het gegeven antwoord goed is of fout.

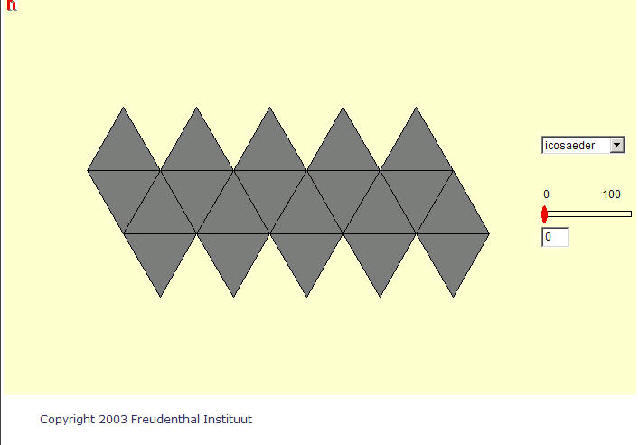
In de rubriek Training vinden de leerlingen de leeropdrachten, afkomstig van het bekende Freudenthal Instituut. Zo moeten ze als eerste opdracht van de gegeven veelvlakken bouwplaten maken voor een piramide, een kubus en nog één naar keuze. Ze krijgen een zogeheten Java-Applet voorgezet met de tekst: ‘kies met de knoppen een van de vijf platonische lichamen. Het lichaam wordt draaiend afgebeeld, met de rotatie-as loodrecht. Deze as kan naar keuze worden veranderd door de knop "Rotatie veranderen" aan te klikken. De kijkhoek is te veranderen door in het gelijknamige tekstveld "Kijkhoek" de waarde te veranderen: van 90° (recht van boven kijken) tot -90° (recht van onderen kijken). De animatie is te pauzeren, of weer op te starten, met de knop "pauze / verder". Bij Training 2 staat een Cloze-activiteit. De leerlingen bestuderen het Wikipedia-artikel uit Oriëntatie. Ze moeten de onbrekende woorden of getallen invullen in een gegeven tabel. Deze digitale driedimensionale presentatie en verwerking van de leereenheid over ruimtefiguren heeft het grote voordeel dat de leerlingen ook daadwerkelijk de ruimte zien en deze met hun muis kunnen manipuleren. Vanuit een leerboek en op een traditioneel schoolbord zou dat niet kunnen.

Pythagoras in de praktijk
Auteur Jacqueline van de Lee-Bosch laat de leerlingen zich eerst kort oriënteren op de toepassingen van de oude stelling van Pythagoras. Hierbij ontbreken ook de leerdoelen niet. Als warming up laat de auteur met een aantal plaatjes zien dat je ‘Pythagoras’ overal tegenkomt. Na enkele interactieve vragen over getoonde ruimtevormen, komt het echte werk. In 2 lesuren moeten de leerlingen aan de computer zelfstandig en individueel vijf opdrachten op een blaadje uitvoeren en inleveren bij hun docent. De opdrachten zijn alle uit te voeren met de stelling van Pythagoras, zoals opdracht 2: ‘Een toren heeft een plat dak in de vorm van een rechthoek. De zijden van die rechthoek zijn 7 bij 11 meter. In één van de hoeken is een antennemast geplaatst. Vanaf een punt, dat 14 meter boven het dak ligt, is deze mast door kabels met de drie andere hoekpunten verbonden. Bereken de lengte van de drie kabels’. 

Aanzichten
Onder het motto: ‘bekijk het eens van een andere kant’, arrangeren de auteurs Jacqueline van de Lee-Bosch en Tom de Koning leermateriaal waarmee de leerlingen interactief individueel of in tweetallen aan de slag kunnen. Na de gebruikelijke onderdelen >oriëntatie, leerdoel, aanpak, beginnen de leerlingen aan de 20 opdrachten van de oefening ‘huisjes draaien’, afkomstig van WisWeb, de website van het Freudenthal Instituut voor het voortgezet onderwijs. Daarna moeten de leerlingen zelf aanzichten bouwen. Ook deze opdrachten zijn afkomstig van WisWeb.

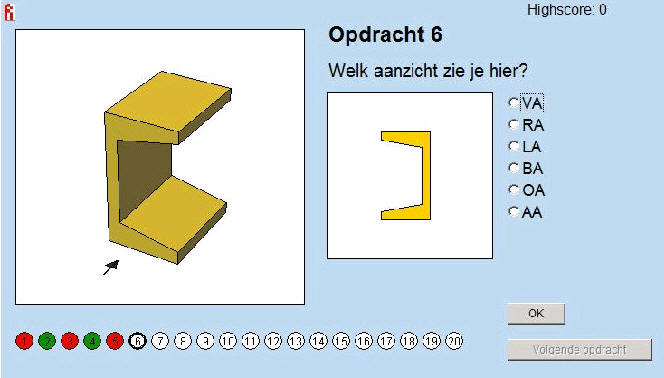
In de eindtoets gaan de leerlingen aanzichten raden. Ook deze opdrachten komen van het Freudenthal Instituut. De leerlingen moeten het linker aanzicht zo draaien dat de figuur gelijk is aan dat van de rechter. Dan moeten ze wel onthouden hebben naar welke kant ze de figuur hebben gedraaid, want ze moeten daarna kiezen welk aanzicht dit is. Tenslotte mogen de leerlingen zelf in een extra opdracht een aanzicht van een voorwerp tekenen waarbij een ander moet raden wat dit is.

Positieve en negatieve getallen

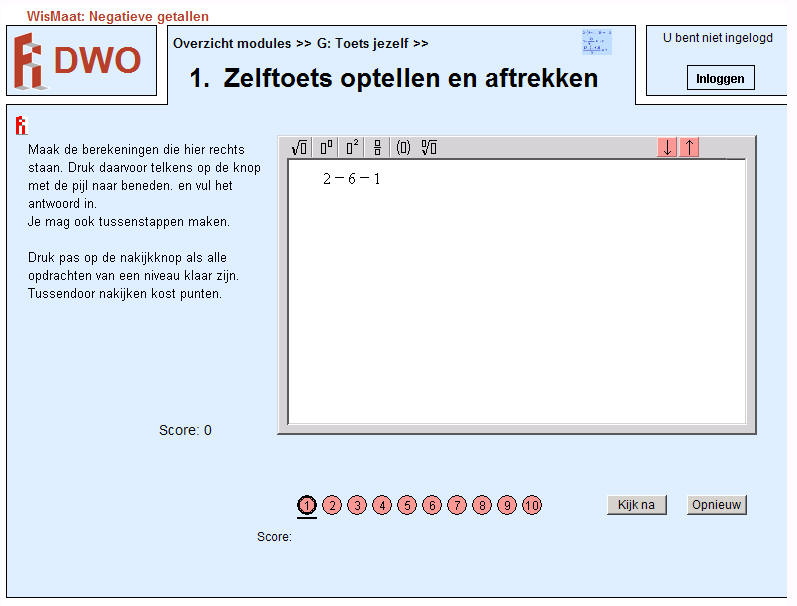
Auteur Hendrik-Jan Timmerije laat de leerlingen na een korte oriëntatie op het onderwerp een starttest maken bij WisMaat, een verzameling digitaal leermateriaal, eveneens ontwikkeld door het Freudenthal Instituut. Als hun score 9 of hoger is, moeten ze dit aantonen met een schermafdruk daarvan. Bij een lagere score moeten ze extra oefenen om dan daarna in de eindtoets aan hun docent te laten zien dat ze daarvan iets hebben geleerd. Wie deze vorm van hoofdrekenen met negatieve en positieve getallen moeilijk vindt, kan eerst oefenen bij de heks, die met blauwe blokjes de temperatuur in haar ketel verhoogt en met rode blokjes deze verlaagt.

Na zoveel oefenen als nodig is om het rekenen met positieve en negatieve getallen onder de knie te krijgen, maken de leerlingen tenslotte een ‘zelftoets’, waarvan de score bepaalt of ze dit onderdeel naar behoren zelfstandig in opdracht van de leermateriaalarrangeur en met hulp van de WisMaat-docenten hebben uitgevoerd. De eigen docent kan aan de ingeleverde schermafdruk van de goede en verkeerde antwoorden van een slecht scorende leerling heel eenvoudig de foute gedachtegang van de leerlingen zien. Een leerling die bijvoorbeeld consequent de dubbele min in 0- - 9 verkeerd interpreteert en als uitkomst -9 invult, zal aan een korte uitleg van zijn docent genoeg hebben om deze fout niet meer te maken.

Een pionier
De OVC heeft als uitgangspunt het arrangeren van bestaand digitaal leermateriaal en zou dus heel goed gebruik kunnen maken van het werk van pionier Hanling Tan, docent wiskunde aan de OSG De Meergronden in Almere. Hij onderhoudt voor zijn vak de eigen website, die voor iedereen gratis toegankelijk is op http://www.xs4all.nl/~sch80729/meergronden/wiskunde/index.html. In het rolmenu links kunnen bezoekers een havo of vwo klas kiezen. Dat verschil bestaat niet voor de eerste en tweede klassen. Na de keus voor een klas volgt die voor een onderwerp.

 

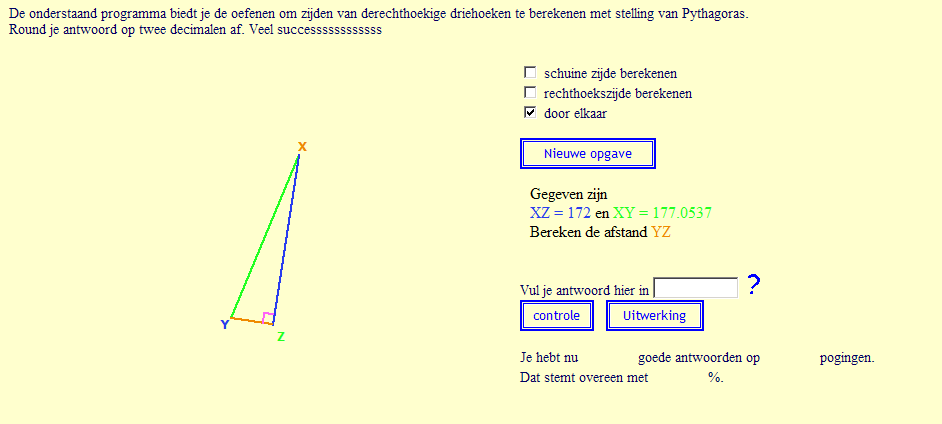
Ook Hanling Tan heeft voor de 2^e klassers interactieve berekeningen geprogrammeerd die zijn gebaseerd op de stelling van Pythagoras. De leerlingen vullen hun antwoord in online, kunnen het controleren en zien meteen hun score. Het zijn oefeningen die de leerlingen zelfstandig en individueel kunnen doen als aanvulling op die van de arrangeur van de OVC. Hanling Tan vult zijn digitaal wiskundeprogramma nog steeds aan totdat het ook leerboekvervangend zal zijn. Dat geldt ook voor het hele programma van Natuur en Techniek van de OVC waarvan wiskunde voor de onderbouw slechts een onderdeel is. (Wordt vervolgd)

omhoog